palais de la découverte
PALAIS DE LA Découverte

Plus d’informations sur notre site internet.
Niveau scolaire : de CE2 à Terminale
Devenez un.e mathématicien.ne en herbe le temps d’une séance d’atelier ! A partir de situations ludiques, venez constater que vous êtes, comme tout le monde, capables de chercher (et trouver !) en mathématiques, chacun à son rythme, chacun à son niveau.
Trois ateliers différents vous sont proposés tout au long du salon.
Si vous êtes enseignant, il est nécessaire d’inscrire votre classe avant le 25 mai.
Si vous êtes un individuel, il suffit de vous connecter à l’horaire indiqué.
Dans les deux cas, attention : chaque atelier nécessite un matériel spécifique (léger) à préparer en amont !!!
POUR LES SCOLAIRES
Les ateliers ont lieu le jeudi 27 mai et le vendredi 28 mai. Il y a une session de chaque atelier chaque demi-journée. (cf-tableau ci-contre)
Il faut impérativement vous inscrire avant le 25 mai, en nous contactant ici : maths.palais@salon.fr
Merci de préciser dans votre mail l’atelier et l’horaire que vous souhaitez.

- LES TRIANGLES MAGIQUES
Durée : 45 minutes
Public : à partir de 9 ans.
Matériel exigé : pions (bouts de papier, jetons, bouchons, etc.) numérotés de 1 à 9, plateau ( support carton, feuille papier, etc.)
Effectif : 8 personnes.
Médiatrice : Sabrina Coudry
Horaires pour les individuels :
– Samedi 29 mai à 14h et 16h.
– Dimanche 30 mai à 11h et 16h.

- QUELLE EST LA QUESTION ?
Durée : 45 minutes
Public : à partir de 9 ans
Matériel exigé : papier, crayons, et si possible un bac à jouets ou une caisse de bricolage pas trop loin, on ne sait jamais !
Effectif : sans limite.
Médiateur : Robin Jamet
Horaires pour les individuels :
– Samedi 29 mai à 15h.
– Dimanche 30 mai à 14h.

- BRICOLAGES MATHÉMATIQUES
Durée : 45 minutes
Public : à partir de 9 ans
Matériel exigé : des bandes de papier, des ciseaux, des crayons, du scotch
Effectif : 8 personnes
Médiateur : Guillaume Reuiller
Horaires pour les individuels :
– Dimanche 30 mai à 10h et 15h.

Durée : 45 minutes
Médiateurs : Robin Jamet et Pablo Idda
Les ondes sont présentes partout : sons, tremblements de terre, lumière des étoiles… L’analyse harmonique est un chapitre des mathématiques permettant de les décortiquer, de les analyser, aussi complexes soient-elles. Discussion entre théoriciens et utilisateurs, à la frontière des mathématiques et de leurs applications. (Voir nos contenus sur l’analyse de Fourier, ci-dessous)
Durée : 45 minutes
Médiateurs : Sabrina Coudry et Robin Jamet de l’unité Mathématiques, Jacques Petitpré de l’unité Physique.
Lors du dernier Salon déMATHérialisé, nous vous avions présenté un “cabinet de curiosités mathématiques” virtuel. Cette année, nous vous en présentons un vrai, en direct depuis le nouveau site des Étincelles-Palais de la découverte, qui a ouvert ses portes en juin !
Durée : 45 minutes
Médiateurs : Sabrina Coudry, Robin Jamet et Guillaume Reuiller
- L'analyse de Fourier à la carte


Résumons avec humour l’analyse de Fourier grâce à ces photos d’Ursus Wehrli : l’idée est de retrouver dans un signal (ici le bol de fruits) ses constituants, ainsi que leurs proportions.
L’analyse de Fourier est une technique mathématique mise au point au 18ème siècle, à l’origine pour résoudre des problèmes physiques. Elle s’est, depuis, largement développée et diversifiée, sous le nom plus général d’analyse harmonique. Le champ de recherche est encore vaste, et les applications pratiques ne se comptent plus, des géosciences à la musique, en passant par le traitement de l’image ou encore la physique quantique.

Qu’il s’agisse d’images, de sons ou d’autres objets d’étude, l’idée est de trouver un ensemble d’éléments particulièrement simples (une base) permettant de reconstituer n’importe quel objet. Les couleurs primaires (jaune magenta cyan pour la peinture, Rouge Vert Bleu (ou “RVB”) pour les ordinateurs) permettent ainsi de coder n’importe quelle couleur (notre objet complexe). Il suffit pour cela d’indiquer les “dosages” de chaque couleur primaire (les coefficients), qui sont ici des valeurs entières comprises entre 0 et 255.
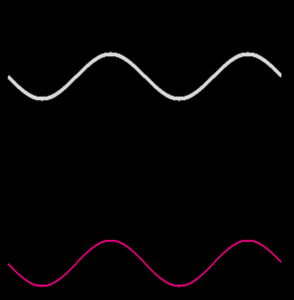
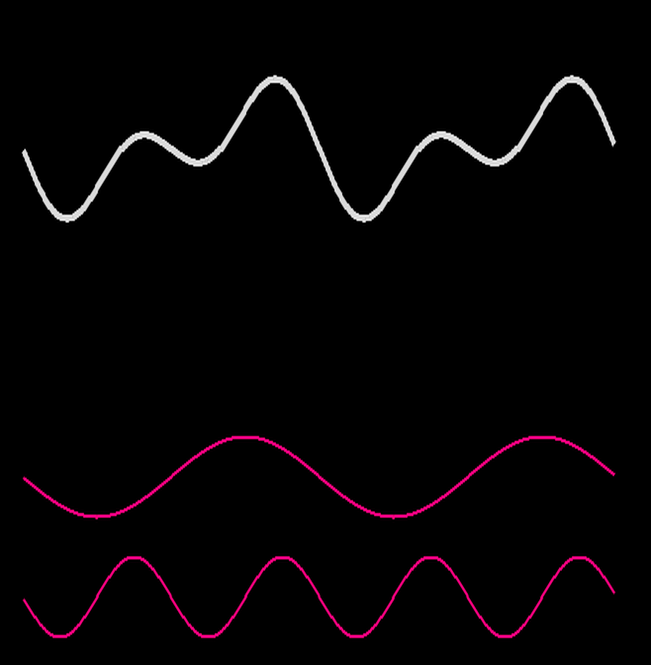
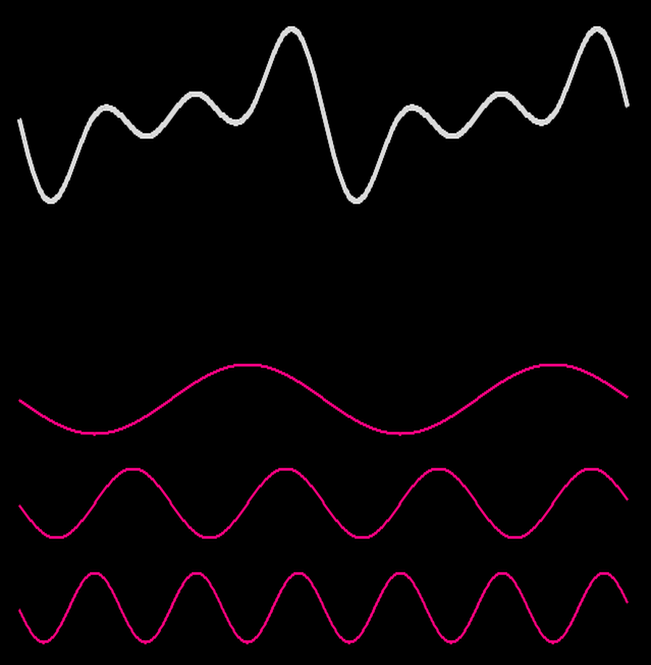
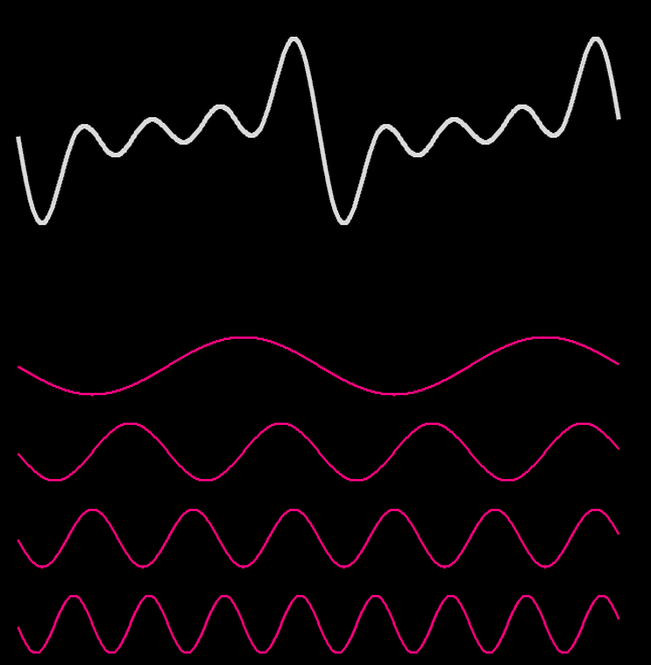
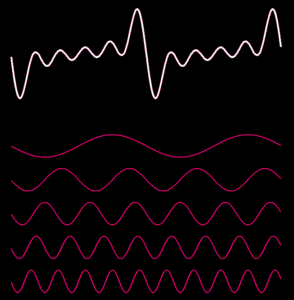
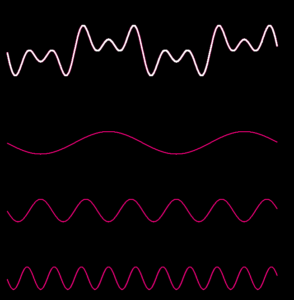
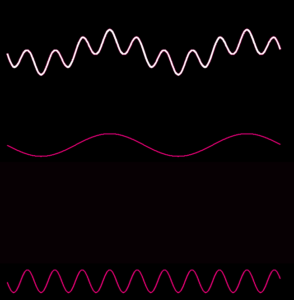
Fourier a trouvé cette idée dans un cadre très différent : l’étude physique de la diffusion de la chaleur. Sans rentrer dans les détails, il montre alors que toute fonction “périodique” (qui se répète) peut s’écrire comme somme de fonctions particulièrement simples : des sinus. Les illustrations ci-dessous montrent intuitivement ce que cela signifie : la fonction plus ou moins compliquée en haut est obtenue en additionnant toutes les fonctions simples au dessous. Pour reprendre les mots de Fourier : “Ce mouvement peut toujours être décomposé en plusieurs autres dont chacun s’accomplit comme s’il avait lieu seul. Cette superposition des effets simples est un des éléments fondamentaux de la théorie de la chaleur.”